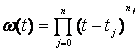29  апреля  2004 г.

А.В. Мерлин (Чувашский  университет)

Сингулярные интегральные уравнения в классе несуммируемых функций

Абстракт.

Рассматриваются сингулярные интегральные уравнения (с.и.у.) с ядром Коши на гладком составном контуре , не содержащем бесконечно удаленной точки. Решения этих уравнений ищутся в классе функций  вида , где 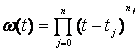,  ,  – достаточное число раз дифференцируемая функция,  удовлетворяющая условию Гельдера. При этом если все , то интегралы, входящие в с.и.у., понимаются в смысле главного значения. Если же >, , , то сингулярные интегралы типа Коши  понимаются  как  частные производные от интеграла по параметру .

            Метод решения с.и.у. есть метод аналитического продолжения в плоскость комплексного переменного, состоящий в сведении с.и.у. к эквивалентной краевой задаче Римана.

            Получено общее решение с.и.у. и исследована картина его разрешимости. Показана возможность применения подобного подхода к с.и.у. с логарифмическим и степенным ядром.